A test (n=1) of weight loss during running

There are reasons why different runners might best adopt 'slightly' different pacing strategies (profiles), even in flat corner-free road marathons, to get their optimal times - if it is critical to maintain a constant metabolic rate in skeletal muscle. One of the reasons has to do with physics, the other physiology. I thought I would try and calculate what that optimal pacing profile (for that 'mythical' flat wind-free cool road marathon) might look like for me. Just how much of a change in pace should I be aiming for if I were to make the very best use of my skeletal muscle carbohydrate stores? [The real world importance of this may be limited since it is possible that I am not limited by my carbohydrate reserves at the pace I can sustain and other runners may fail to make the best of their reserves because they start too quickly in the first place.]

It is well known that increases in muscle power-output disproportionately consume carbohydrate reserves. The reason is that the relationship between carbohydrate usage relative to fat usage is highly non-linear with pace. Since carbohydrate stores in skeletal muscle are limited, and once they are 'exhausted' fat metabolism remains as the only option and it has a relatively low rate of energy production. Thus, it is also widely accepted that near flat power-output (or metabolic rate) - of an appropriate power that 'exhausts' the carbohydrate stores by the end of the marathon - also results in the best performance.

Thus, we arrive at the question; "What should the pace profile look like to achieve that flat power-output?". There are two main factors that I think we need to consider - "How does weight change during the marathon?" and "How does efficiency change during the marathon?" If weight decreases during the marathon then a steady power output should result in a proportional increase in speed (and vice versa). If efficiency decreases (which is likely) then speed will need to decrease for a constant power output to be maintained.

I thought I would do a little n=1 experiment to test this on myself. It is a reasonably good example of how a very simple set of measurements can help us address questions of pacing. The equipment I have used is easily and cheaply available and accessible to anyone wanting to investigate how they respond. Your response may be different - but, probably not that much different from a weight-scaled version of me.

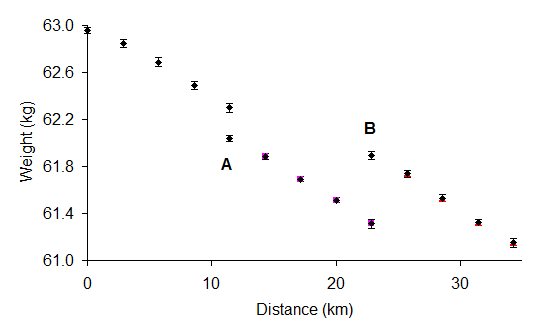
This evening I did a sequence of 12 laps (2.86 km; see Strava) whilst weighing myself between each lap). I used a Salter Ultimate Accuracy domestic scales (they read to 50g) - which I had previously calibrated. I weighed myself 8 times in succession at each lap using an 'anti-defeat' protocol (these scales do not register a new weight unless it is more that ~200g different from the last one, so I alternated holding a 1.74 kg weight). I was wearing leggings, heavy trainers and a long sleeve base layer (no hat, gloves or jacket). The clothes were chosen to limit radiant heat loss but allow sweat evapouration. All weights were made wearing these clothes. The weather was mild (~13C) but the wind was reasonably strong. I set out at 4:57 mins per km pace and attempted to minimize pace and heart rate deviations - however, the wind and lack of lighting made this difficult. After each lap I returned inside and at the entrance weighed myself (it took ~2 min to make the 8 measurements). I did not use a towel or drip sweat - all weight loss, other than where indicated - was evaporative.

The graph of my weight (mean+/-SD) against distance is plotted in Figure 1. At point A I emptied my bladder and bowel and at point B I consumed (rapidly) roughly a pint of water - exact weights in figure legend. The step changes in weight were planned. As expected there was a gradual loss of weight, although careful observation reveals that at the start, after point A and after point B the first weight loss appears smaller.

Figure 1. Weight measured at 2.86 km intervals. Each data point consists of eight measurements (mean+/-SD). At point A I went to the toilet where I lost 263g (urine and faeces), I weighed myself before and after. At point B I consumed  581g tap water again weighing myself before and after.

To look at the weight changes in more detail I have plotted the absolute weight loss over the course of each lap in Figure 2. The open symbols show the first lap and the laps after the pause for the toilet (A) and after drinking (no pause but the consumption of room temperature water, B). With each lap I lost on average 177g of water (or 62g per km). This represents a weight loss of 0.1% of my body weight per km travelled and if scaled over a whole marathon would be 2.6 kg for me (~60kg). This is a bit less than the 3.15 kg I lost at Frankfurt (although there was a time lag between the race and the measurements in that case). This weight loss (4.2% of body weight over the course of a marathon is in agreement with the faster runners in published studies). The 0.1% decrease in body weight would require an equivalent increase in speed to keep muscle power output constant - i.e. 0.3 s per km increase in pace with each km. For a marathon at this pace it would mean starting at 4:57 per km and finishing at 4:45 per km creating a ~2 min negative split.

Figure 2. Weight change over the course of each lap plotted against distance.

However, it is possible that running becomes progressively less efficient and that the effect is to require greater muscle power to produce the same speed. The weight loss data should allow us to investigate this. Evaporatiing water carries away 0.54 kcal per g. In Figure 3 I have used this number to calculate the total evaporative metabolic energy loss - the best representation of muscle power that we can calculate with these data. To make this calculation I have assumed an incremental efficiency of 21% through out. The legend contains details of the calculation.

.

Figure 3. Data from Figure 2 replotted as the metabolic rate supported by evaporation in kcal per kg of body weight per km covered. To calculate this I took the weight of water lost and divided it by the body weight and by the distance travelled whilst multiplying it by the latent heat of vaporization (540 cal per g) and dividing it by 0.79 since 21% of the energy is lost as useful mechanical work (79% is lost as the waste heat by the water loss).

The metabolic rate supported by evaporation is approximately 0.8 kcal per kg of body weight per km. This is lower than the standard value of 1 kcal per kg per km which is widely cited within the literature (and used by some GPS watches to calculate calorific cost) since some heat is lost through radiation. Assuming the radiant heat loss remains constant throughout the run, any increase in this value represents a loss of efficiency. Indeed, there might be a slight upward trend in my data suggesting a loss in efficiency. Fitting the data with a straight line yields a slope of 0.25% per km. If this same loss of efficiency were to occur in the marathon this would more than offset the negative split suggested by the weight loss. However, I did not taper for this run and I am at the end of a 180km week only two weeks after a marathon - so I am unlikely to be as robust as I would going into a race. The other confounding factor here is that I consumed a pint of water which I would not in a marathon - this negated some of the weight loss.

Unfortunately the dataset is not good enough to detect the changes in efficiency on the step change loss or gain in weight (toilet and drink) - more data points or a large weight change might be necessary - and perhaps better pacing to reduce the noise. It is by no means perfect. But, I am pleased with the amount of information that can be extracted from such a simple test.

So, to conclude. Weight loss seems to occur at a rate of about 0.1% per km suggesting an optimal pace might be a negative split, but this might be offset by a potential decrease in efficiency of 0.25%, something which suggests an optimal pace might be a 2 min positive split. But, the precise value will depend upon the temperature (i.e. sweating rate) and the rate of decrease in efficiency. The 'take home' message is probably that near flat pace - for someone who does NOT drink during the marathon might be best. If you drink and gain weight during the marathon and your efficiency declines faster then a positive split profile (i.e. slowing from the very start) might be optimal for the fastest possible marathon. However, for less well trained runners there are likely to be more important factors at play. I will investigate this further in my next post.